SAP Hana Vora Stock Trading
08 Dec 2016 | Raul PuriOne crucial element that all statistical learning algorithms need is the ability to handle a tremendous amount of data very quickly. People have used different frameworks for querying, or fetching, data. Among these include Hadoop’s MapReduce framework and the Apache Spark framework. SAP Hana Vora’s (HV) unique in-memory Hadoop query engine for MapReduce frameworks is a promising new tool for big data and performing analysis in a distributed fashion on large databases of information. We demonstrate HV’s potential as a powerful resource for ML by examining its performance on tasks such as stock prediction on market data. We also contributed some additional functionality to the SAP HV library in the process.

Raul Puri, Akash Khosla, Christoph Shache, Ishan Dikshit, Rahil Mathur, Michael Tu, Rishi Satoor, Zhongxia Yan, Phillip Kuznetsov
Backtesting and Data set
Every algorithm needs testing…
We started off implementing our stock predictor in HV by focusing on what we’d be using to test and train our stock predictor. We used Quantopian’s backtesting platform for trading algorithms to test the predictor. Quantopian’s platform uses the quandl test dataset for testing, which contains trading history from prior years. An example of their basic dataset we used:
{"timestamp":{"s":"1478808720"},"open":{"s":"90.5"},"symbol":{"s":"PM"},"volume":{"s":"32582"},"high":{"s":"90.5"},"low":{"s":"90.4499969482"},"close":{"s":"90.4499969482"}}
It also needs a large amount of training data…
Quantopian additionally provides Quandl’s training and validation datasets as a public resource for training. We’ve pulled the training dataset and stored it appropriately in a SQL Database. However, in order to augment our dataset for training purposes and ensure our stock predictor generalizes well to numerous situations, we set up a data scraper on Amazon Web Services (AWS) to continuously pull additional data from Bloomberg’s services and expand our existing SQL DataBase of training data.
The Stock Trading Algorithm
Recent approaches to creating stock predictor algorithms have leveraged Deep Q Learning to learn a function to approximate the profit (rewards) received from executing buy and sell operations given input data about stock history. We follow this approach; however, we relaxed the problem by learning a simpler linear function for these predictions (as opposed to a deep neural network). For our input data, we took the current stock information and the output from the last time step, allowing us to use recurrent patterns in the problem and build a simple linear model that also has an attention component.
We used HV’s map reduce capabilities to compute all our buy/sell actions in a training batch by computing a linear operation on all the input data (minus the recurrent information about the last action). After this we used a prefix sum scan to then performed the linear operation on the recurrent component of our input data. We then computed the resulting rewards and used this information to optimize our learned reward approximation function. Given large training batch sizes, this allows us to develop a training system that is able to efficiently distribute large amounts of computation.
Our Contribution to Hana Vora
The Prefix Sum…
The prefix sum is an operation on a list of number defined by:
\(y_0 = x_0\)
\(y_1 = x_0 + x_1\)
\(y_2 = x_0 + x_1 + x_2\)
\(...\)
Parallelizing the prefix sum with HV…
The prefix sum is an inherently serial algorithm, so this can produce bottlenecks in performance even if all other computations are done in parallel with MapReduce. As a result, we can leverage MapReduce with a graph-like computation structure (see hidden visualization) to efficiently parallelize this inherently serial function. We implemented this algorithm with modularity in mind, so it can be generalized to run on any kernel that can describe the reduce steps in the below algorithm (eg. it can work on prefix multiplication by swapping a \(x+y\) kernel with a \(x•y\) kernel). The parallelization of this algorithm is a relevant contribution to Hana Vora as it opens up the possibility for other functions such as an exponential moving average, Markov models, etc.
Upsweep
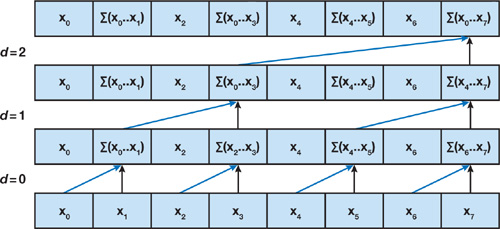
for \(d = 0\) to \(log_{2}(n-1)\) do
for all \(k=0\) to \(n-1\) by \(2^{d}+1\) in parallel do
\(x[k+2^{d+1}-1]=x[k+2^{d}-1]+x[k+2^{d+1}-1]\)
Downsweep
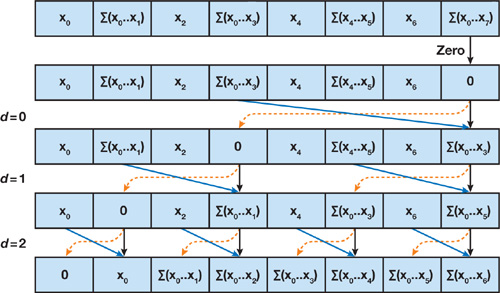
\(x[n-1] \leftarrow 0\)
for \(d=log_{2}{n-1}\) down to 0 do
for all \(k=0\) to \(n-1\) by \(2^{d}+1\) in parallel do
\(t=x[k+2^{d}-1]\)
\(x[k+2^{d}-1]=x[k+2^{d+1}-1]\)
\(x[k+2^{d+1}-1]=t+x[k+2^{d+1}-1]\)
Future Considerations
More ML functionality for HV…
Hana Vora shows promise because it was fast and performed well when parallelizing our analysis of stock data and training our stock predictor. Given the foundation that we have laid in this semester and more time, we would like to leverage Hana Vora’s timeseries capability to produce more complex models for modeling stock analysis: utilizing techniques such as hidden Markov models. Additionally, we’d like to try and implement something equivalent to a resilient distributed dataset support (RDD) for Hana Vora so it can perform better on tasks such as matrix computation, giving it a further edge as a tool for ML and opening up more areas of exploration and use for Hana Vora.
